Série 7

Figure sinxlex.asy

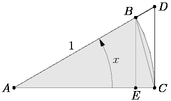
import geometry;

size(0,100);
real theta=30;

pair A=(0,0); 
pair B=dir(theta);
pair C=(1,0);
pair D=(1,Tan(theta));
pair E=(Cos(theta),0);

filldraw(A--C{N}..B--cycle,lightgrey);
draw(B--C--D--cycle);
draw(B--E);

draw("$x$",arc(C,A,B,0.7),RightSide,Arrow,PenMargin);

dot("$A$",A,W);
dot("$B$",B,NW);
dot("$C$",C);
dot("$D$",D);
dot(("$E$"),E,S);
label("$1$",A--B,LeftSide);
      

Figure spheresilhouette.asy

import solids;
settings.render=0;
settings.prc=false;

size(200);

revolution r=sphere(O,1);
draw(r,1,longitudinalpen=nullpen);
draw(r.silhouette());

Figure spiral.asy

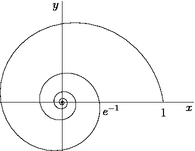
size(0,150);
import graph;

real f(real t) {return exp(-t/(2pi));}

draw(polargraph(f,0,20*pi,operator ..));

xaxis("$x$",-infinity,1.3);
yaxis("$y$",-infinity,1);

labelx(1);
labelx("$e^{-1}$",1.0/exp(1),SE);

Figure spline.asy

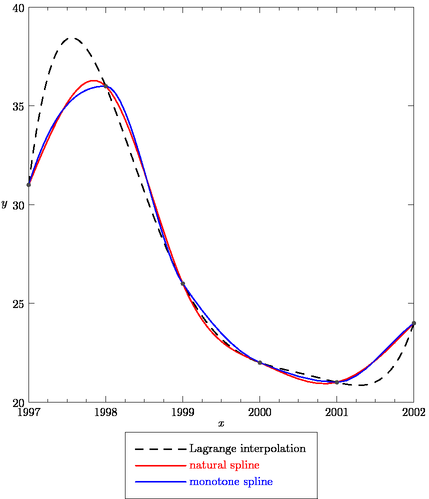
import graph; 
import interpolate; 
 
size(15cm,15cm,IgnoreAspect); 
 
real a=1997, b=2002; 
int n=5; 
real[] xpt=a+sequence(n+1)*(b-a)/n; 
real[] ypt={31,36,26,22,21,24}; 
horner h=diffdiv(xpt,ypt);
fhorner L=fhorner(h);
 
scale(false,true);

pen p=linewidth(1);

draw(graph(L,a,b),dashed+black+p,"Lagrange interpolation");
draw(graph(xpt,ypt,Hermite(natural)),red+p,"natural spline");
draw(graph(xpt,ypt,Hermite(monotonic)),blue+p,"monotone spline");
xaxis("$x$",BottomTop,LeftTicks(Step=1,step=0.25));
yaxis("$y$",LeftRight,RightTicks(Step=5));

dot(pairs(xpt,ypt),4bp+gray(0.3));

attach(legend(),point(10S),30S);

Figure spring0.asy

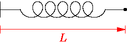
import spring;

drawspring(0,"$L$");

Figure spring2.asy

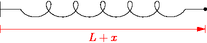
import spring;

drawspring(40.0,"$L+x$");

Figure star.asy

size(100);
import math;

int n=5;
path p;

int i=0;
do {
  p=p--unityroot(n,i);
  i=(i+2) % n;
} while(i != 0);

filldraw(p--cycle,red+evenodd);

Figure strokepath.asy

path g=scale(100)*unitcircle;
pen p=linewidth(1cm);

frame f;
// Equivalent to draw(f,g,p):
fill(f,strokepath(g,p),red);
shipout("strokepathframe",f);
shipped=false;

size(400);

// Equivalent to draw(g,p):
currentpicture.add(new void(frame f, transform t) {
    fill(f,strokepath(t*g,p),red);
  });
currentpicture.addPath(g,p);