Série 1

Figure advection.asy

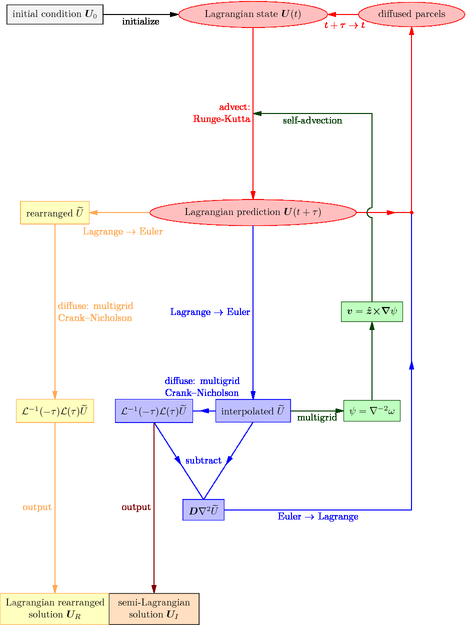
size(0,22cm);

texpreamble("
\usepackage{bm}
\def\v{\bm}
\def\grad{\v\nabla}
\def\cross{{\v\times}}
\def\curl{\grad\cross}
\def\del{\nabla}
");

defaultpen(fontsize(10pt));

real margin=1.5mm;

object IC=draw("initial condition $\v U_0$",box,(0,1),
               margin,black,FillDraw(palegray));
object Adv0=draw("Lagrangian state $\v U(t)$",ellipse,(1,1),
                 margin,red,FillDraw(palered));
object Adv=draw("Lagrangian prediction $\v U(t+\tau)$",ellipse,(1,0),
                margin,red,FillDraw(palered));
object AdvD=draw("diffused parcels",ellipse,(1.8,1),
                 margin,red,FillDraw(palered));
object Ur=draw("rearranged $\v \widetilde U$",box,(0,0),
               margin,orange+gray,FillDraw(paleyellow));
object Ui=draw("interpolated $\v \widetilde U$",box,(1,-1),
               margin,blue,FillDraw(paleblue));
object Crank=draw("${\cal L}^{-1}(-\tau){\cal L}(\tau)\v \widetilde U$",
                  box,(0.5,-1),margin,blue,FillDraw(paleblue));
object CrankR=draw("${\cal L}^{-1}(-\tau){\cal L}(\tau)\v \widetilde U$",
                   box,(0,-1),margin,orange+gray,FillDraw(paleyellow));
object Urout=draw(minipage("\center{Lagrangian rearranged solution~$\v U_R$}",
                           100pt),box,(0,-2),margin,orange+gray,
                  FillDraw(paleyellow));
object Diff=draw("$\v D\del^2 \v \widetilde U$",box,(0.75,-1.5),
                 margin,blue,FillDraw(paleblue));
object UIout=draw(minipage("\center{semi-Lagrangian solution~$\v U_I$}",80pt),
                  box,(0.5,-2),margin,FillDraw(palered+paleyellow));
object psi=draw("$\psi=\del^{-2}\omega$",box,(1.6,-1),
                margin,darkgreen,FillDraw(palegreen));
object vel=draw("$\v v=\v{\hat z} \cross\grad\psi$",box,(1.6,-0.5),
                margin,darkgreen,FillDraw(palegreen));

add(new void(frame f, transform t) {
    pair padv=0.5*(point(Adv0,S,t)+point(Adv,N,t));
    picture pic;
    draw(pic,"initialize",point(IC,E,t)--point(Adv0,W,t),RightSide,Arrow,
         PenMargin);
    draw(pic,minipage("\flushright{advect: Runge-Kutta}",80pt),
         point(Adv0,S,t)--point(Adv,N,t),RightSide,red,Arrow,PenMargin);
    draw(pic,Label("Lagrange $\rightarrow$ Euler",0.45),
         point(Adv,W,t)--point(Ur,E,t),5LeftSide,orange+gray,
         Arrow,PenMargin);
    draw(pic,"Lagrange $\rightarrow$ Euler",point(Adv,S,t)--point(Ui,N,t),
         RightSide,blue,Arrow,PenMargin);
    draw(pic,point(Adv,E,t)--(point(AdvD,S,t).x,point(Adv,E,t).y),red,
         Arrow(Relative(0.7)),PenMargin);
    draw(pic,minipage("\flushleft{diffuse: multigrid Crank--Nicholson}",80pt),
         point(Ui,W,t)--point(Crank,E,t),5N,blue,MidArrow,PenMargin);
    draw(pic,minipage("\flushleft{diffuse: multigrid Crank--Nicholson}",80pt),
         point(Ur,S,t)--point(CrankR,N,t),LeftSide,orange+gray,Arrow,PenMargin);
    draw(pic,"output",point(CrankR,S,t)--point(Urout,N,t),RightSide,
         orange+gray,Arrow,PenMargin);
    draw(pic,point(Ui,S,t)--point(Diff,N,t),blue,MidArrow,PenMargin);
    draw(pic,point(Crank,S,t)--point(Diff,N,t),blue,MidArrow,PenMargin);
    label(pic,"subtract",point(Diff,N,t),12N,blue);
    draw(pic,Label("Euler $\rightarrow$ Lagrange",0.5),
         point(Diff,E,t)--(point(AdvD,S,t).x,point(Diff,E,t).y)--
         (point(AdvD,S,t).x,point(Adv,E,t).y),RightSide,blue,
         Arrow(position=1.5),PenMargin);
    dot(pic,(point(AdvD,S,t).x,point(Adv,E,t).y),red);
    draw(pic,(point(AdvD,S,t).x,point(Adv,E,t).y)--point(AdvD,S,t),red,Arrow,
         PenMargin);
    draw(pic,"output",point(Crank,S,t)--point(UIout,N,t),RightSide,brown,Arrow,
         PenMargin);
    draw(pic,Label("$t+\tau\rightarrow t$",0.45),
         point(AdvD,W,t)--point(Adv0,E,t),2.5LeftSide,red,Arrow,PenMargin);
    draw(pic,point(psi,N,t)--point(vel,S,t),darkgreen,Arrow,PenMargin);
    draw(pic,Label("self-advection",4.5),point(vel,N,t)--
         arc((point(vel,N,t).x,point(Adv,E,t).y),5,270,90)--
         (point(vel,N,t).x,padv.y)--
         padv,LeftSide,darkgreen,Arrow,PenMargin);
    draw(pic,Label("multigrid",0.5,S),point(Ui,E,t)--point(psi,W,t),darkgreen,
         Arrow,PenMargin);

    add(f,pic.fit());
  });

Figure alignbox.asy

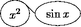
real margin=1.5mm;

object left=align(object("$x^2$",ellipse,margin),W);
add(left);
object right=align(object("$\sin x$",ellipse,margin),4E);
add(right);
currentpicture.add(new void(frame f, transform t) {
    draw(f,point(left,NE,t)--point(right,W,t));
  });

Figure alignedaxis.asy

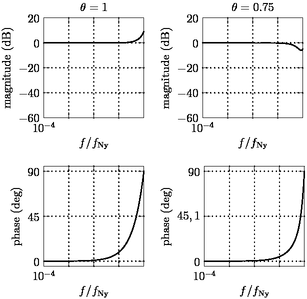
import graph;

real Freq=60.0;
real margin=5mm;

pair exp(pair x) {
  return exp(x.x)*(cos(x.y)+I*sin(x.y));
}

real Merr(real x, real w) {
  real tau=x/(2*Freq);
  return 20*log(abs((tau*w+tau/(exp(I*2*pi*Freq*tau)-1))*(I*2*pi*Freq)));
}

real Aerr(real x, real w) {
  real tau=x/(2*Freq);
  return degrees((tau*w+tau/(exp(I*2*pi*Freq*tau)-1))*(I*2*pi*Freq));
}

picture pic1;
scale(pic1,Log,Linear);
real Merr1(real x){return Merr(x,1);}
draw(pic1,graph(pic1,Merr1,1e-4,1),black+1.2);

ylimits(pic1,-60,20);
yaxis(pic1,"magnitude (dB)",LeftRight,RightTicks(new
                                                 real[] {-60,-40,-20,0,20}));
xaxis(pic1,"$f/f_\mathrm{Ny}$",BottomTop,LeftTicks(N=5));
yequals(pic1,0,Dotted);
yequals(pic1,-20,Dotted);
yequals(pic1,-40,Dotted);
xequals(pic1,1e-3,Dotted);
xequals(pic1,1e-2,Dotted);
xequals(pic1,1e-1,Dotted);

size(pic1,100,100,point(pic1,SW),point(pic1,NE));

label(pic1,"$\theta=1$",point(pic1,N),2N);

frame f1=pic1.fit();
add(f1);

picture pic1p;
scale(pic1p,Log,Linear);
real Aerr1(real x){return Aerr(x,1);}
draw(pic1p,graph(pic1p,Aerr1,1e-4,1),black+1.2);

ylimits(pic1p,-5,95);
yaxis(pic1p,"phase (deg)",LeftRight,RightTicks(new real[] {0,45,90}));
xaxis(pic1p,"$f/f_\mathrm{Ny}$",BottomTop,LeftTicks(N=5));
yequals(pic1p,0,Dotted);
yequals(pic1p,45,Dotted);
yequals(pic1p,90,Dotted);
xequals(pic1p,1e-3,Dotted);
xequals(pic1p,1e-2,Dotted);
xequals(pic1p,1e-1,Dotted);

size(pic1p,100,100,point(pic1p,SW),point(pic1p,NE));

frame f1p=pic1p.fit();
f1p=shift(0,min(f1).y-max(f1p).y-margin)*f1p;
add(f1p);

picture pic2;
scale(pic2,Log,Linear);
real Merr2(real x){return Merr(x,0.75);}
draw(pic2,graph(pic2,Merr2,1e-4,1),black+1.2);

ylimits(pic2,-60,20);
yaxis(pic2,"magnitude (dB)",LeftRight,RightTicks(new
                                                 real[] {-60,-40,-20,0,20}));
xaxis(pic2,"$f/f_\mathrm{Ny}$",BottomTop,LeftTicks(N=5));
yequals(pic2,0,Dotted);
yequals(pic2,-20,Dotted);
yequals(pic2,-40,Dotted);
xequals(pic2,1e-3,Dotted);
xequals(pic2,1e-2,Dotted);
xequals(pic2,1e-1,Dotted);

size(pic2,100,100,point(pic2,SW),point(pic2,NE));

label(pic2,"$\theta=0.75$",point(pic2,N),2N);

frame f2=pic2.fit();
f2=shift(max(f1).x-min(f2).x+margin)*f2;
add(f2);

picture pic2p;
scale(pic2p,Log,Linear);
real Aerr2(real x){return Aerr(x,0.75);}
draw(pic2p,graph(pic2p,Aerr2,1e-4,1),black+1.2);

ylimits(pic2p,-5,95);
yaxis(pic2p,"phase (deg)",LeftRight,RightTicks(new real[] {0,45.1,90}));
xaxis(pic2p,"$f/f_\mathrm{Ny}$",BottomTop,LeftTicks(N=5));
yequals(pic2p,0,Dotted);
yequals(pic2p,45,Dotted);
yequals(pic2p,90,Dotted);
xequals(pic2p,1e-3,Dotted);
xequals(pic2p,1e-2,Dotted);
xequals(pic2p,1e-1,Dotted);

size(pic2p,100,100,point(pic2p,SW),point(pic2p,NE));

frame f2p=pic2p.fit();
f2p=shift(max(f1p).x-min(f2p).x+margin,min(f2).y-max(f2p).y-margin)*f2p;
add(f2p);

Figure buildcycle.asy

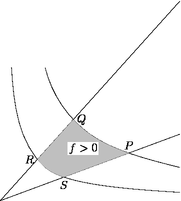
size(200);

real w=1.35;

path[] p;
for(int k=0; k < 2; ++k) {
  int i=2+2*k;
  int ii=i^2;
  p[k]=(w/ii,1){1,-ii}::(w/i,1/i)::(w,1/ii){ii,-1};
}

path q0=(0,0)--(w,0.5);
path q1=(0,0)--(w,1.5);
draw(q0); draw(p[0]); draw(q1); draw(p[1]);
path s=buildcycle(q0,p[0],q1,p[1]);
fill(s,mediumgrey);

label("$P$",intersectionpoint(p[0],q0),N);
label("$Q$",intersectionpoint(p[0],q1),E);
label("$R$",intersectionpoint(p[1],q1),W);
label("$S$",intersectionpoint(p[1],q0),S);
label("$f > 0$",0.5*(min(s)+max(s)),UnFill);

Figure cardioid.asy

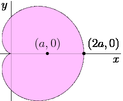
import graph;

size(0,100);

real f(real t) {return 1+cos(t);}

path g=polargraph(f,0,2pi,operator ..)--cycle;
filldraw(g,pink);

xaxis("$x$",above=true);
yaxis("$y$",above=true);

dot("$(a,0)$",(1,0),N);
dot("$(2a,0)$",(2,0),N+E);

Figure centroidfg.asy

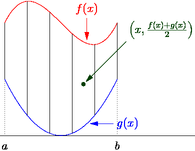
import graph;
size(0,150);

int a=-1, b=1;

real f(real x) {return x^3-x+2;}
real g(real x) {return x^2;}

draw(graph(f,a,b,operator ..),red);
draw(graph(g,a,b,operator ..),blue);
 
xaxis(); 

int n=5;

real width=(b-a)/(real) n;
for(int i=0; i <= n; ++i) {
  real x=a+width*i;
  draw((x,g(x))--(x,f(x)));
}
 
labelx("$a$",a);
labelx("$b$",b);
draw((a,0)--(a,g(a)),dotted);
draw((b,0)--(b,g(b)),dotted);

real m=a+0.73*(b-a);
arrow("$f(x)$",(m,f(m)),N,red);
arrow("$g(x)$",(m,g(m)),E,0.8cm,blue);

int j=2;
real xi=b-j*width;
real xp=xi+width;
real xm=0.5*(xi+xp);
pair dot=(xm,0.5*(f(xm)+g(xm)));
dot(dot,darkgreen+4.0);
arrow("$\left(x,\frac{f(x)+g(x)}{2}\right)$",dot,NE,2cm,darkgreen);

Figure circles.asy

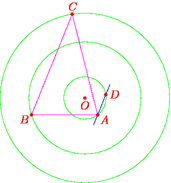
size(6cm,0);
import math;

currentpen=magenta;

real r1=1;
real r2=sqrt(7);
real r3=4;
pair O=0;

path c1=circle(O,r1);
draw(c1,green);
draw(circle(O,r2),green);
draw(circle(O,r3),green);

real x=-0.6;
real y=-0.8;
real yD=0.3;
pair A=(sqrt(r1^2-y^2),y);
pair B=(-sqrt(r2^2-y^2),y);
pair C=(x,sqrt(r3^2-x^2));

pair d=A+r2*dir(B--C);
pair D=intersectionpoint(c1,A--d);

draw(A--B--C--cycle);
draw(interp(A,D,-0.5)--interp(A,D,1.5),blue);

dot("$O$",O,S,red);
dot("$A$",A,dir(C--A,B--A),red);
dot("$B$",B,dir(C--B,A--B),red);
dot("$C$",C,dir(A--C,B--C),red);
dot("$D$",D,red);

Figure coag.asy

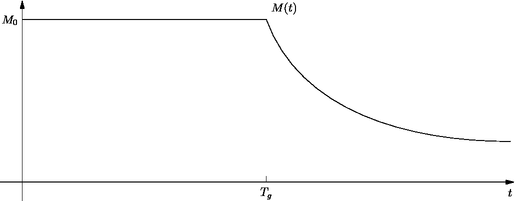
size(0,200);
import graph;

pair z0=(0,0);
pair m0=(0,1);
pair tg=(1.5,0);
pair mt=m0+tg;
pair tf=(3,0);

draw(m0--mt{dir(-70)}..{dir(0)}2tg+m0/4);
xtick("$T_g$",tg,N);
label("$M(t)$",mt,2NE);
labely("$M_0$",m0);

xaxis(Label("$t$",align=2S),Arrow);
yaxis(Arrow);