Semaine 8, L2 Algèbre
3 décembre 2007Conséquences. PGCD, PPCM, Lemme de Gauss, Lemme d’Euclide, Théorème de Bezout, Algorithme d’Euclide pour les polynômes.
Décomposition en produit de facteurs irréductibles. Théorème. Tout polynôme non irréductible unitaire se décompose de manière unique à l’ordre près en un produit de polynômes irréductibles unitaires.
Corollaire. Version non unitaire.
Remarque. Version où on regroupe les facteurs irréductibles identiques.
Théorème. Les polynômes de degré 1 sont irréductibles.
IV] Racines
1) Fonction polynôme. définition, définition de racine d’un polynôme
Théorème. 
est racine de 
si et seulement 
divise .
Extension. racine multiple.
Théorème. décomposition d’un polynôme selon les racines que l’on connait.
Corrolaire. Un polynôme de degré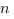 
admet au plus 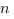racines.
Cas complexe.
Théorème de d’Alembert Gauss. Tout polynôme à coefficient complexe de degré supérieur à 1 admet au moins une racine complexe.
Corollaire. Les seuls polynômes complexes irréductibles sont de degré 1.
Conséquence. Tout polynôme complexe se factorise en 
.
(ou la version où on regroupe les racines communes).
Cas réel
Partant du fait que 
est irréductible dans ![bbR delim{[}{X}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_bc8c69d27474df149f2468f9f7f9a9ef.png "bbR delim{[}{X}{]}")
on cherche à déterminer les polynômes irréductibles réels.
Proposition. Si ![P in bbR delim{[}{X}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_2f37da310f716cf2f7b5dfd072be92f6.png "P in bbR delim{[}{X}{]}")
alors pour tout 
on
a 
.