Semaine 8, L2 Intégrales
3 décembre 2007Théorème. Si 
et 
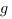sont positives et équivalentes au voisinage de 
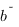alors 
et 
sont de même nature.
Application 1 Soit localement intégrable sur 
.
-
S’il existe
tel que
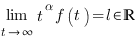alors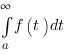 
converge.
- S’il existe
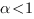tel que
alors 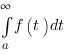diverge.
Remarque. Chercher deux exemples de fonctions telles que 
tend vers 0 en l’infini avec
dans un cas l’intégrale convergente et dans l’autre l’intégrale divergente. (exemple donner en cours).
Applications 2. l’analogue mais comportement en 0.
III] Fonctions quelconques.
Remarque, exemple Sans information sur le signe tout devient plus dur. En effet on peut trouver deux fonctions équivalentes à l’infini mais avec des intégrales n’étant pas de même nature.
1) Intégration par partie. sous quelle condition a-t-on le droit de faire une intégration par partie avec des intégrales généralisées ?
2) Changement de variables. Idem
3) Règle d’Abel. (le truc de la dernière chance !)
Théorème. Soit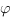 
définie de dans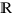 
continue par morceaux telle que
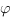- positive
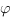- décroissante
-
tend vers 0 en l’infini.
Soit une fonction continue sur le même intervalle telle qu’il existe 
vérifiant : pour tout 
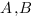on a 
.
Alors 
converge.
Lemme. Une autre formule de la moyenne.