Edt L3, semestre 2
janvier 26th, 2008
Comme promis, le voici edtl3math.pdf et la version officielle (ajout de cours) ici
Intégrale, exos 1 et 2, sept 2007
décembre 25th, 2007
Voici une correction rapide, attention c’est du AsciiMathML, I.E. (sans plugin) s’abstenir !
Exercice 1 (a) Pour tout $p$ la fonction $x^{p}/(1+x^{2})$ est définie continue sur $[0,1]$, donc intégrable. Pour $I_{0}$ on reconnaît la fameuse $\arctan$ et pour $I_{1}$ c’est facile $$ I_{0}=\arctan x\Big]_{0}^{1}=\frac{\pi}{4},\qquad I_{1}=-\frac{\ln(1+x^{2})}{2}\Big]_{0}^{1}=\frac{\ln(2)}{2}.$$
(b) Quelques calculs : $$ I_{p}+I_{p+2}=\int_{0}^{1} \frac{x^{p}+x^{p+2}}{1+x^{2}} dx= \int_{0}^{1} x^{p}\frac{1+x^{2}}{1+x^{2}}dx=\int_{0}^{1}x^{p}dx= \frac{1}{p+1}.$$ On utilise alors cette relation pour avoir d’une part $I_{0}+I_{2}=1$ soit $I_{2}=1-\pi/4$ et d’autre part $I_{1}+I_{3}=1/2$ soit $I_{3}=(1-\ln(2))/2$.
(c) (visiblement c’est une récurrence) on connaît $I_{2}$, regardons $v_{1}$ ! Clairement $v_{1}=(-1)^{2}/(2*1-1)=1$ ! D’où $v_{1}+(-1)^{1}I_{2}=\pi/4$, la récurrence est initiée ! Supposons désormais l’égalité vraie au rang $q$ (avec $q\geq 1$) et montrons qu’elle est vérifiée au rang $q+1$ : d’après la question (b) et la définition de $v_{n}$ nous avons successivement $$ I_{2q+2}=\frac{1}{2q+1}-I_{2q},\qquad v_{q+1}=v_{q}+\frac{(-1)^{q+1+1}}{2(q+1)-1} $$ $$ v_{q+1}+(-1)^{q+1}I_{2q+2}=v_{q}+\frac{(-1)^{q}}{2q+1}+\frac{(-1)^{q+1}}{2q+1}+(-1)^{q}I_{2q} =\frac{\pi}{4} \qquad[(-1)^{2}=1.]$$ Ce qui permet de conclure.
(d) Pour tout $x\in[0,1]$, on a $x^{2}+1\geq 1$ d’où, $\frac{x^{p}}{1+x^{2}}\leq x^{p}$ sur $[0,1]$. Les propriétés usuelles des intégrales permettent d’affirmer que pour tout $p\in\N$ on a $$ 0\leq I_{p}\leq \int_{0}^{1}x^{p}dx \leq \frac{1}{p+1}, $$ ce qui entraîne : $\lim_{p\rightarrow +\infty}I_{p}=0$. Avec la question (c) on en déduit alors que $v_{n}$ admet $\pi/4$ comme limite quand $n$ tend vers l’infini.
(e) (ici deux comportements contraires, l’idée avec l’intégration par partie est de compenser la présence de $p$ en intégrant le $x^{p}$ pour faire apparaître un $1/(p+1)$) On écrit $$ pI_{p}=\int_{0}^{1}\frac{px^{p}}{1+x^{2}}dx=\frac{px^{p+1}}{(p+1)(x^{2}+1)}\Big]_{0}^{1} + \frac{p}{p+1}\int_{0}^{1}\frac{2x^{p+2}}{(1+x^{2})^{2}}dx=\frac{p}{2(p+1)}+ \frac{p}{p+1}\int_{0}^{1}\frac{2x^{p+2}}{(1+x^{2})^{2}}dx.$$ Clairement la quantité $\frac{p}{2(p+1)}$ tend vers $1/2$ quand $p$ tend vers l’infini. Pour le dernier terme on procède comme dans la question (d). L’encadrement $$ 0\leq \frac{p}{p+1}\int_{0}^{1}\frac{2x^{p+2}}{(1+x^{2})^{2}} dx \leq \int_{0}^{1} 2x^{p+2}dx\leq \frac{2}{p+3}$$ permet de conclure que $\lim_{p\rightarrow \infty}pI_{p}=1/2$.
Exercice 2.
(a) Comme $f$ est dérivable en $0$ et que $f(0)=0$ alors $$ \lim_{t\rightarrow 0^{+}} h(t)= \lim_{t\rightarrow 0^{+}} \frac{f(t)}{t}=f’(0)=\alpha,\quad \lim_{t\rightarrow 0^{+}} g(t)= \lim_{{t\rightarrow 0^{+}}}\frac{f(t)}{\sqrt{t}}=\lim_{{t\rightarrow 0^{+}}}\sqrt{t}\frac{f(t)}{{t}}=0. $$
(b) Un simple calcul : $ \forall t>0,\qquad f’(t)-\sqrt{t}g’(t)=\frac{h(t)}{2}.$
(c) Comme $\sqrt{t}g’(t)=f’(t)-h(t)/2$, $\forall t>0$, et comme $f’$ est continue on déduit de la question (a) que $\lim_{t\rightarrow 0^{+}}\sqrt{t}g(t)=\alpha/2$. On peut tout écrire en fonction de $f$ ou encore écrire que, $\forall t>0$, $$ g(t)g’(t)=\frac{g(t)}{\sqrt{t}} \sqrt{t}g’(t)=h(t) \sqrt{t}g’(t), $$ d’où $\lim_{t\rightarrow 0^{+}} g(t)g’(t)=\frac{\alpha^{2}}{2}$.
(d) Pour établir (1) il faut d’une part bien voir que l’on intègre sur $]0,x]$ des fonctions définies sur $]0,\infty[$ et d’autre part se sortir des calculs. Dans la question (c) on a démontré que $\sqrt{t}g’(t)$ et $g’(t)g(t)$ étaient prolongeables par continuité en $0$ (de même d’ailleurs pour $h(t)$ et $g’(t)$). Toutes les intégrales de (1) sont donc bien définies a priori. Par précaution, soient $x>\varepsilon>0$ : la question (b) donne avec intégration sur $[\varepsilon,x]$ $$ \int_{\varepsilon}^{x} (f(t))^{2}dt - \int_{\varepsilon}^{x} (\sqrt{t}g’(t))^{2}dt = \int_{\varepsilon}^{x} (f’(t) -\sqrt{t}g’(t))(f’(t) +\sqrt{t}g’(t))dt = = \int_{\varepsilon}^{x} \frac{h(t)}{2}\Big(\frac{h(t)}{2}+2\sqrt{t}g’(t)\Big) dt $$ $$ =\frac{1}{4}\int_{\varepsilon}^{x} (h(t))^{2}dt + \int_{\varepsilon}^{x}\frac{f(t)}{\sqrt{t}}{g’(t)}dt = \frac{1}{4}\int_{\varepsilon}^{x} (h(t))^{2}dt + \int_{\varepsilon}^{x}g(t)g’(t)dt = \frac{1}{4}\int_{\varepsilon}^{x} (h(t))^{2}dt + \frac{1}{2} (g(t))^{2}\Big]_{\varepsilon}^{x}.$$ Pour conclure il suffit de faire tendre $\varepsilon\rightarrow0$ et d’écrire que les fonctions $\sqrt{t}g’(t)$, $h(t)$ (donc leur carré) sont prolongeables par continuité en $0$, ainsi les intégrales convergent et l’égalité (1) est démontrée.
(e) Les termes du membres de droite de (1) sont tous positifs. Ainsi comme $\int_{0}^{\infty}(f’(t))^{2}dt$ est convergente, on a pour tout $x>0$ $$ \int_{0}^{x}\Big(\frac{f(t)}{t}\Big)^{2}dt \leq \int_{0}^{x}(f’(t))^{2}dt \leq \int_{0}^{\infty}(f’(t))^{2}dt. $$ La fonction $\Big(\frac{f(t)}{t}\Big)^{2}$ étant positive, l’inégalité précédente permet de conclure.
Semaine 9, L2 Algèbre
décembre 4th, 2007
Caractérisation des polynômes irréductibles de ![bbR delim{[}{X}{]} bbR delim{[}{X}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_bc8c69d27474df149f2468f9f7f9a9ef.png) : les polynômes de degré 1 et les polynômes de degré 2 n’admettant pas de racine réelle.
: les polynômes de degré 1 et les polynômes de degré 2 n’admettant pas de racine réelle.
V] Polynôme dérivé — lien avec les racines multiples.
1) Polynôme dérivé. définition, propriétés
Dérivées successives, dérivée k-ème de  .
.
Formule de Leibniz (non démontrée)
Polynôme composé
Formule de Taylor pour un polynôme.
2) Lien entre zéros multiples et dérivée
Si  est racine de
est racine de  d’ordre
d’ordre  ,
, 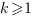 alors
alors  est racine de
est racine de  d’ordre
d’ordre  .
.
Attention pour la réciproque il faut savoir que  est racine de
est racine de  .
.
Théorème.  admet
admet  comme racine d’ordre
comme racine d’ordre  (
(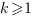 ) si et seulement si les polynômes
) si et seulement si les polynômes  ,…,
,…,  admettent
admettent  comme racine et
comme racine et 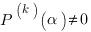 .
.
Bonus track
Relations entre les zéros d’un polynôme et ses coefficients.
Semaine 8, L2 Algèbre
décembre 3rd, 2007
Conséquences. PGCD, PPCM, Lemme de Gauss, Lemme d’Euclide, Théorème de Bezout, Algorithme d’Euclide pour les polynômes.
Décomposition en produit de facteurs irréductibles. Théorème. Tout polynôme non irréductible unitaire se décompose de manière unique à l’ordre près en un produit de polynômes irréductibles unitaires.
Corollaire. Version non unitaire.
Remarque. Version où on regroupe les facteurs irréductibles identiques.
Théorème. Les polynômes de degré 1 sont irréductibles.
IV] Racines
1) Fonction polynôme. définition, définition de racine d’un polynôme
Théorème.  est racine de
est racine de  si et seulement
si et seulement  divise
divise  .
.
Extension. racine multiple.
Théorème. décomposition d’un polynôme selon les racines que l’on connait.
Corrolaire. Un polynôme de degré 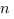 admet au plus
admet au plus 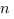 racines.
racines.
Cas complexe.
Théorème de d’Alembert Gauss. Tout polynôme à coefficient complexe de degré supérieur à 1 admet au moins une racine complexe.
Corollaire. Les seuls polynômes complexes irréductibles sont de degré 1.
Conséquence. Tout polynôme complexe se factorise en  .
(ou la version où on regroupe les racines communes).
.
(ou la version où on regroupe les racines communes).
Cas réel
Partant du fait que  est irréductible dans
est irréductible dans ![bbR delim{[}{X}{]} bbR delim{[}{X}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_bc8c69d27474df149f2468f9f7f9a9ef.png) on cherche à déterminer les polynômes irréductibles réels.
on cherche à déterminer les polynômes irréductibles réels.
Proposition. Si ![P in bbR delim{[}{X}{]} P in bbR delim{[}{X}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_2f37da310f716cf2f7b5dfd072be92f6.png) alors pour tout
alors pour tout  on
a
on
a  .
.
Semaine 8, L2 Intégrales
décembre 3rd, 2007
Théorème. Si  et
et 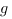 sont positives et équivalentes au voisinage de
sont positives et équivalentes au voisinage de 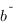 alors
alors  et
et  sont de même nature.
sont de même nature.
Application 1 Soit  localement intégrable sur
localement intégrable sur  .
.
-
S’il existe
 tel que
tel que
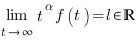 alors
alors 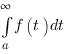 converge.
converge.
- S’il existe
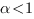 tel que
tel que
 alors
alors 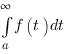 diverge.
diverge.
Remarque. Chercher deux exemples de fonctions telles que  tend vers 0 en l’infini avec
dans un cas l’intégrale convergente et dans l’autre l’intégrale divergente. (exemple donner en cours).
tend vers 0 en l’infini avec
dans un cas l’intégrale convergente et dans l’autre l’intégrale divergente. (exemple donner en cours).
Applications 2. l’analogue mais comportement en 0.
III] Fonctions quelconques.
Remarque, exemple Sans information sur le signe tout devient plus dur. En effet on peut trouver deux fonctions équivalentes à l’infini mais avec des intégrales n’étant pas de même nature.
1) Intégration par partie. sous quelle condition a-t-on le droit de faire une intégration par partie avec des intégrales généralisées ?
2) Changement de variables. Idem
3) Règle d’Abel. (le truc de la dernière chance !)
Théorème. Soit 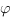 définie de
définie de  dans
dans 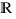 continue par morceaux telle que
continue par morceaux telle que
-
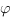 positive
positive -
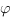 décroissante
décroissante -
 tend vers 0 en l’infini.
tend vers 0 en l’infini.
Soit  une fonction continue sur le même intervalle telle qu’il existe
une fonction continue sur le même intervalle telle qu’il existe  vérifiant : pour tout
vérifiant : pour tout 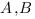 on a
on a  .
.
Alors  converge.
converge.
Lemme. Une autre formule de la moyenne.
Semaine 7, L2 Intégrales
décembre 3rd, 2007
II) Convergence des intégrales de fonctions positives
Théorème.  est intégrable au sens généralisée
sur
est intégrable au sens généralisée
sur 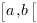 si et seulement si la fonction
si et seulement si la fonction
 est bornée sur
est bornée sur 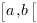 .
.
Remarque. Si  est positive et
est positive et  diverge
alors
diverge
alors  tend vers l’infini quand
tend vers l’infini quand 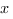 tend vers
tend vers
 .
.
1) Intégrales de Références. (à savoir, comme le reste)
Intégrales de Riemann et intégrales de Bertrand.
Remarque contre-exemple. si  est positive et
est positive et  convergente alors
convergente alors  n’admet pas nécessairement une limite en l’infini !
n’admet pas nécessairement une limite en l’infini !
2) Comparaison.
Théorème. Si  et
et 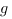 sont positives telles que
sont positives telles que  alors
alors
a)  converge entraîne
converge entraîne 
b) la contraposée de a)
3) Critère de domination et d’équivalence.
Rappel. O, o (notation de Landau) ou domination, équivalence de fonctions.
Théorème. Si  et
et 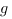 sont positives telles que
sont positives telles que  en
en 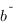 alors
alors
 converge entraîne
converge entraîne  converge.
converge.
Semaine 6, L2 Intégrales
novembre 15th, 2007
Extension. Définition de l’intégrale généralisée aux 2 bornes
Proposition. Une fonction  définie (et localement intégrable) de
définie (et localement intégrable) de ![delim{]}{a,b}{[} delim{]}{a,b}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_d3435d355c9a2a5496f0497a517ed497.png) dans
dans
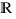 est intégrable au sens généralisé sur
est intégrable au sens généralisé sur ![delim{]}{a,b}{[} delim{]}{a,b}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_d3435d355c9a2a5496f0497a517ed497.png) si et seulement si
il existe
si et seulement si
il existe  et
et 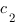 tels que les intégrales généralisées
tels que les intégrales généralisées  et
et  existent.
existent.
Proposition. idem ssi  l’est sur
l’est sur ![delim{]}{a,c}{]} delim{]}{a,c}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_4538ac73fb018ce36967509874b374d4.png) et sur
et sur 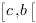 pour tout
pour tout 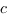 dans
dans ![delim{]}{a,b}{[} delim{]}{a,b}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_d3435d355c9a2a5496f0497a517ed497.png) .
.
Extension : intégrales plusieurs fois impropres
Remarque. méthodologie
Proposition. Si  est bornée sur
est bornée sur 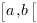 et localement intégrable on peut
prolonger
et localement intégrable on peut
prolonger  en une fonction intégrable sur
en une fonction intégrable sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) et donc
et donc  est intégrable au sens généralisé sur
est intégrable au sens généralisé sur 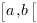 .
.
2) Critère de Cauchy pour les intégrales généralisées — convergence absolue
Théorème.  est intégrable au sens généralisé si et seulement si elle vérifie
le critère de Cauchy.
est intégrable au sens généralisé si et seulement si elle vérifie
le critère de Cauchy.
Définition. Qu’est-ce qu’une intégrale généralisée absolue convergente ?
Définition. Absolument convergente entraîne convergente.
Remarque. Réciproque fausse, exemple donné en cours.
3) Propriétés diverses sur les combinaisons linéaires d’intégrales (absolument) convergentes.
Semaine 7, L2 Algèbre
novembre 15th, 2007
NOUVEAU CHAPITRE : LES POLYNÔMES
I] Définition 1) Définition d’un polynôme
Définitions (avec la suite infinie d’éléments du corps  dont
les éléments sont tous nuls à partir d’un certain rang), polynôme nul, dégré valuation, égalité
de deux polynômes
dont
les éléments sont tous nuls à partir d’un certain rang), polynôme nul, dégré valuation, égalité
de deux polynômes
2) Opérations sur les polynômes
Somme, produit interne, multiplication par un scalaire
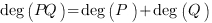 C’est un anneau commutatif intègre.
C’est un anneau commutatif intègre.
3) Notation définitive
Écriture avec des  (Ouf !)
(Ouf !)
Définition Coefficient dominant, polynôme unitaire, les constantes.
II) Les deux divisions
Rappels sur la divisibilté
Division euclidienne ou suivant les puissances décroissantes non démontré, exemple détaillé
Division suivant les puissances croissantes à l’ordre  non démontré, exemple détaillé
non démontré, exemple détaillé
III) ![K delim{[}{X}{]} K delim{[}{X}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_e165207f929c508d4851a9ea058ea3ac.png) Anneau principal — PGCD — PPCM — irréductible
Anneau principal — PGCD — PPCM — irréductible
Théorème ![K delim{[}{X}{]} K delim{[}{X}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_e165207f929c508d4851a9ea058ea3ac.png) est un anneau principal + unicité si on impose
le polynôme unitaire.
est un anneau principal + unicité si on impose
le polynôme unitaire.
Semaine 6, L2 Algèbre
novembre 13th, 2007
Proposition.  divise
divise  si et seulement si
si et seulement si 
Définition Qu’est-ce que deux éléments associés ?
Définition Qu’est-ce qu’un idéal principal ?
Définition Qu’est-ce qu’un anneau principal ?
PGCD, PPCM, élément irréductible dans un anneau intègre
Définitions. PGCD et PPCM d’une famille d’éléments.
Remarque. il n’est pas démontrer que le PGCD et PPCM existent !
Définition. Éléments premiers entre eux, élément irréductible.
Cas des anneaux principaux
Dans un anneau principal le PGCD et PPCM de deux éléments (non nuls) existent et est unique à une association près. De plus on a l’identité de Bezout.
Lemmes de Gauss, Euclide
PGCD, PPCM dans  .
Division euclidienne et algorithme d’Euclide. (fin laborieuse !)
.
Division euclidienne et algorithme d’Euclide. (fin laborieuse !)
Semaine 5, L2 Intégrales
octobre 30th, 2007
suite et fin : Inégalité de Taylor-Lagrange
V) Interprétation géométrique et calcul approché.
1) Aire (algèbrique) du domaine 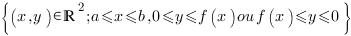 représente
représente  .
.
2)Calcul approché, méthode des rectangles et des trapèzes, estimations de l’erreur sous des hyphothèses
de régularité sur  .
.
Chapitre 2 — Intégrales généralisées ou intégrales impropres
Intégrales généralisées.
1) Définitions.
Soit  une fonction définie de l’intervalle
une fonction définie de l’intervalle 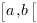 dans
dans  avec
avec  ou
ou  . On dit que
. On dit que
 est localement intégrable sur
est localement intégrable sur 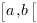 si pour tout
si pour tout 
 est intégrable
est intégrable ![delim{[}{a,c}{]} delim{[}{a,c}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_dbb7ec04d57ea50d102eedaa2ba62a6c.png) .
.
Définition. (intégrale une seule fois impropre) Soit  une fonction localement intégrable
sur
une fonction localement intégrable
sur 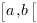 . On dit que
. On dit que  est intégrable au sens généralisé de Riemann si
est intégrable au sens généralisé de Riemann si
 existe. On note cette limite
existe. On note cette limite 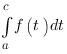 .
.
Remarque. Si  est Riemann intégrable sur l’intervalle
est Riemann intégrable sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) alors
(bien sûr) la restricition de
alors
(bien sûr) la restricition de  sur
sur 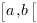 est intégrable au sens généralisé de Riemann.
est intégrable au sens généralisé de Riemann.
Remarque. Dans toute la suite (exercice, examen, etc) il faudra montrer que l’existence de cette intégrale généralisée avant tout calcul, manipulation, etc.
Remarque. Définition analogue pour un intervalle du type ![delim{]}{a,b}{]} delim{]}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_8993f49c76604f04cbf547b0afc1c131.png) avec
avec
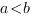 ou
ou  .
.
Page suivante »
