Semaine 7, L2 Intégrales
3 décembre 2007II) Convergence des intégrales de fonctions positives
Théorème.  est intégrable au sens généralisée
sur
est intégrable au sens généralisée
sur 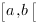 si et seulement si la fonction
si et seulement si la fonction
 est bornée sur
est bornée sur 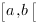 .
.
Remarque. Si  est positive et
est positive et  diverge
alors
diverge
alors  tend vers l’infini quand
tend vers l’infini quand 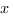 tend vers
tend vers
 .
.
1) Intégrales de Références. (à savoir, comme le reste)
Intégrales de Riemann et intégrales de Bertrand.
Remarque contre-exemple. si  est positive et
est positive et  convergente alors
convergente alors  n’admet pas nécessairement une limite en l’infini !
n’admet pas nécessairement une limite en l’infini !
2) Comparaison.
Théorème. Si  et
et 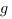 sont positives telles que
sont positives telles que  alors
alors
a)  converge entraîne
converge entraîne 
b) la contraposée de a)
3) Critère de domination et d’équivalence.
Rappel. O, o (notation de Landau) ou domination, équivalence de fonctions.
Théorème. Si  et
et 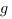 sont positives telles que
sont positives telles que  en
en 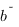 alors
alors
 converge entraîne
converge entraîne  converge.
converge.
