Semaine 6, L2 Intégrales
15 novembre 2007Extension. Définition de l’intégrale généralisée aux 2 bornes
Proposition. Une fonction  définie (et localement intégrable) de
définie (et localement intégrable) de ![delim{]}{a,b}{[} delim{]}{a,b}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_d3435d355c9a2a5496f0497a517ed497.png) dans
dans
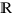 est intégrable au sens généralisé sur
est intégrable au sens généralisé sur ![delim{]}{a,b}{[} delim{]}{a,b}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_d3435d355c9a2a5496f0497a517ed497.png) si et seulement si
il existe
si et seulement si
il existe  et
et 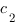 tels que les intégrales généralisées
tels que les intégrales généralisées  et
et  existent.
existent.
Proposition. idem ssi  l’est sur
l’est sur ![delim{]}{a,c}{]} delim{]}{a,c}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_4538ac73fb018ce36967509874b374d4.png) et sur
et sur 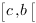 pour tout
pour tout 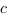 dans
dans ![delim{]}{a,b}{[} delim{]}{a,b}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_d3435d355c9a2a5496f0497a517ed497.png) .
.
Extension : intégrales plusieurs fois impropres
Remarque. méthodologie
Proposition. Si  est bornée sur
est bornée sur 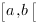 et localement intégrable on peut
prolonger
et localement intégrable on peut
prolonger  en une fonction intégrable sur
en une fonction intégrable sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) et donc
et donc  est intégrable au sens généralisé sur
est intégrable au sens généralisé sur 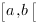 .
.
2) Critère de Cauchy pour les intégrales généralisées — convergence absolue
Théorème.  est intégrable au sens généralisé si et seulement si elle vérifie
le critère de Cauchy.
est intégrable au sens généralisé si et seulement si elle vérifie
le critère de Cauchy.
Définition. Qu’est-ce qu’une intégrale généralisée absolue convergente ?
Définition. Absolument convergente entraîne convergente.
Remarque. Réciproque fausse, exemple donné en cours.
3) Propriétés diverses sur les combinaisons linéaires d’intégrales (absolument) convergentes.
