Semaine 2, L2 Algèbre
3 octobre 2007Bonjour
Voici ce qui a été fait en cours:
Démonstration du Théorème de Lagrange
Définition de l’ordre d’un élément
Groupe quotient
Définition. Une relation d’équivalence  est dite
compatible avec la loi
est dite
compatible avec la loi  si
si  et
et  entraînent
entraînent 
Théorème. Si  est une relation d’équivalence compatible
avec
est une relation d’équivalence compatible
avec  (
( groupe) alors l’ensemble quotient
groupe) alors l’ensemble quotient  muni de la l.c.i,
muni de la l.c.i,  , est un groupe
, est un groupe
Application. Si  est abélien et
est abélien et  sous groupe de
sous groupe de  définition de la relation
modulo
définition de la relation
modulo  (
(  ssi
ssi 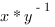 dans
dans  ), compatible avec
), compatible avec  .
.
On note 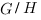 l’ensemble
l’ensemble  , qui est un groupe muni de
la loi définie dans le théorème précédent.
, qui est un groupe muni de
la loi définie dans le théorème précédent.
Description des classes d’équivalence
Exemple (détaillé?!). 
7) Décomposition canonique d’un morphisme de groupe
Théorème. Si morphisme de groupe de
morphisme de groupe de  dans
dans
 (groupes supposés abéliens) alors
(groupes supposés abéliens) alors  et
et  sont isomorphes.
sont isomorphes.
