Semaine 1, L2 Intégrales
5 octobre 2007I] Intégrale et fonctions en escalier
1) Définitions
Définition : subdivision d’une subdivision (ou partage) d’un intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)
Définition : qu’est-ce qu’une fonction en escalier définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 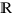 ?
?
Définition : qu’est-ce qu’une subdivision adaptée à une fonction  en escalier
en escalier
Relation d’ordre sur l’ensemble des subdivision d’un intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)
Conséquences : si 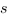 et
et  sont deux subdivisions on définit la plus fine des deux et
la plus grossière des deux. La plus fine étant “grosso-modo” la réunion des deux (attention c’est une suite ordonnée)
et la plus grossière étant l’intersection (nécessairement non vide car les deux extrémités sont des points
de la subdivision).
sont deux subdivisions on définit la plus fine des deux et
la plus grossière des deux. La plus fine étant “grosso-modo” la réunion des deux (attention c’est une suite ordonnée)
et la plus grossière étant l’intersection (nécessairement non vide car les deux extrémités sont des points
de la subdivision).
Propriétés des fonctions en escalier
Il suffit de faire un dessin pour se convaincre que si  sont deux fonctions en escalier sur
sont deux fonctions en escalier sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) et
et  un réel alors
un réel alors
-
 est une fonction en escalier
est une fonction en escalier -
 est une fonction en escalier
est une fonction en escalier -
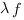 est une fonction en escalier
est une fonction en escalier -
 est une fonction en escalier
est une fonction en escalier
Remarque L’ensemble des fonctions en escalier est une algèbre
2) Intégrale d’une fonction en escalier
Définition Si  est une fonction en escalier et
est une fonction en escalier et  une subdivision adaptée à
une subdivision adaptée à  alors la quantité
alors la quantité
 où
où  est la valeur constante prise par
est la valeur constante prise par  sur l’intervalle
sur l’intervalle ![delim{]}{x_i,x_{i+1}}{[} delim{]}{x_i,x_{i+1}}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_986_65c66e982f749a99da9bfc363d6b9a86.png) , ne dépend que de
, ne dépend que de  et en aucun cas de la subdvision. Cette somme est l’intégrale de
et en aucun cas de la subdvision. Cette somme est l’intégrale de  à
à  de
de  et se note
et se note  .
.
il faut bien voir/comprender/savoir démontrer que la quantité ainsi définie ne dépend
pas de la subdivision choisie !
Propriétés :
- si
 sont deux fonctions en escalier sur
sont deux fonctions en escalier sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) coïncidant sauf en un nombre fini de points alors leur intégrale sur l’intervalle sont égales
coïncidant sauf en un nombre fini de points alors leur intégrale sur l’intervalle sont égales - l’application qui à une fonction en escalier associe son intégrale est une application linéaire
-

- si
 est positive alors son intégrale l’est aussi
est positive alors son intégrale l’est aussi
Relation de Chasles. Comme la restriction d’un fonction en escalier sur ![[a,b] [a,b]](/wordpress/wp-content/plugins/phpmathpublisher/img/math_981_7be3ce2022e25e9c66f71ee324ecc5aa.png) à un sous intervalle est encore en escalier on démontre
à un sous intervalle est encore en escalier on démontre

II] Intégrabilité au sens de Riemann
1) Définition
Définition Soit  une fonction définie de
une fonction définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 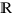 . Cette fonction est dite Riemann-intégrable si et seulement si l’une des deux conditions équivalentes est vérifiée
. Cette fonction est dite Riemann-intégrable si et seulement si l’une des deux conditions équivalentes est vérifiée
- (A) pour tout
 strictement positif il existe
strictement positif il existe  en escalier
sur
en escalier
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) telles que pour tout
telles que pour tout 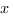 dans
dans ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) on a
on a
 et
et 
- (B) il existe deux suites de fonctions en escalier
 telles que pour tout
telles que pour tout 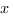 et pour tout
et pour tout 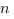 on a
on a
 et
et 
Quand une des propriétés équivalents (A) ou (B) est vérifiée et pour toute suite 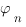 associée à
associée à  définie par (B) on démontre que la quantité
définie par (B) on démontre que la quantité 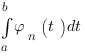 converge vers un réel qui ne dépend pas du choix de la suite
converge vers un réel qui ne dépend pas du choix de la suite 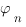 mais qui dépend uniquement de
mais qui dépend uniquement de  et est noté
et est noté
 .
.
Remarque. Si  est en escalier alors elle est intégrable au sens de Riemann (heureusement) et les notations
introduites sont compatibles.
est en escalier alors elle est intégrable au sens de Riemann (heureusement) et les notations
introduites sont compatibles.
Proposition. Si une fonction est Riemann intégrable alors elle est bornée.
Lemme. Soit  une fonction définie de
une fonction définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 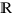 . La fonction
. La fonction  est Riemann intégrable si et seulement si pour tout
est Riemann intégrable si et seulement si pour tout  telles que
telles que
-
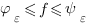 sur
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)
-
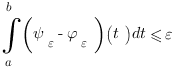
2) Propriétés
- l’application qui à une fonction Riemann-intégrable associe son intégrale est une application linéaire
- Si
 est positive et Riemann intégrable il en est de même pour son intégrale
est positive et Riemann intégrable il en est de même pour son intégrale - si
 est Riemann intégrable alors
est Riemann intégrable alors  est Riemann intégrable et
est Riemann intégrable et

- Si
 est Riemann intégrable et si
est Riemann intégrable et si 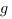 est une fonction égale à
est une fonction égale à  partout (sur
partout (sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) ) sauf en un nombre fini de points alors
) sauf en un nombre fini de points alors 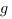 est Riemann intégrable et
est Riemann intégrable et

Remarque : il faut bien comprendre que dans les deux dernières propriétés il y a d’une part une propriété qualitative
( et
et 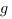 sont Riemann-intégrables) et d’autre part une propriété quantitative (une inégalité et une égalité).
sont Riemann-intégrables) et d’autre part une propriété quantitative (une inégalité et une égalité).
