Semaine 3, L2 Intégrales
16 octobre 2007 III) Fonctions à valeurs complexes
Définition. Soit  une fonction de
une fonction de
![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) à valeurs complexes. La fonction
à valeurs complexes. La fonction
 est intégrable au sens de Riemann si et seulement
est intégrable au sens de Riemann si et seulement
 et
et  (parties réelle et
complexe de la fonction) sont intégrables au sens de Riemann
sur l’intervalle
(parties réelle et
complexe de la fonction) sont intégrables au sens de Riemann
sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) . Dans ce cas on
définit
. Dans ce cas on
définit  .
.
Propriétés. Les propriétés vues précédemment dans le cas des fonctions
à valeurs réelles subsistent. De plus on a l’inégalité pour toute
fonction à valeurs complexes intégrables sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)

IV) Cauchy-Schwarz, Minkowski et inégalité de la moyenne
1) Cauchy-Scwarz et Minkowski
Proposition, inégalité de Cauchy-Schwarz. Soient  et
et
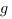 deux fonctions intégrables au sens de Riemann sur l’intervalle
deux fonctions intégrables au sens de Riemann sur l’intervalle
![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) . Alors la fonction
. Alors la fonction  est
intégrable et on a l’inégalité
est
intégrable et on a l’inégalité

Remarque. Le produit de deux fonctions intégrables est intégrable
Proposition, inégalité de Minkowski

2) Inégalité de la moyenne
Proposition. Soient  et
et 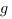 deux fonctions
intégrables au sens de Riemann sur l’intervalle
deux fonctions
intégrables au sens de Riemann sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) telles
que
telles
que  . Alors on a l’inégalité
. Alors on a l’inégalité
 Si de plus
Si de plus  est continue alors il existe
est continue alors il existe ![c in delim{[}{a,b}{]} c in delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_1d6a4d7efe65e3ff39a9e9e4bd1eda6f.png) tel
que
tel
que 
Définition. Soit  une fonction continue sur
une fonction continue sur
![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) (donc intégrable). Alors il existe
(donc intégrable). Alors il existe ![c in delim{[}{a,b}{]} c in delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_1d6a4d7efe65e3ff39a9e9e4bd1eda6f.png) tel
que
tel
que  . Cette quantité est appelée
valeur moyenne de
. Cette quantité est appelée
valeur moyenne de  .
.
