Semaine 4, L2 Algèbre
22 octobre 2007Théorème. Toute permutation se décompose en produit de cycles à supports disjoints. De plus si l’on exclut les
cycles triviaux d’ordre 1, cette décomposition est unique à l’ordre près.
Preuve non faite en cours, idée sur un exemple et document donné pour cette preuve.
Proposition. Les transpositions engendrent l’ensemble des permutations, i.e. toute permutation peut se décomposer
en produit de transposition.
Pour la preuve il suffit de montrer que tout cycle se décompose en produit de transposition et d’utiliser le théorème précédent.
Définition. Qu’est-ce que la signature d’une permutation ? ici on donne la définition via le nombre d’inversion, la signature est notée 
.
Proposition. Si 
sont 
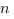réels et 
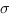une permutation de 
alors
.
Proposition. Si 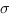et 
sont deux permutations alors 
.
III) Anneaux
1) Définitions. Qu’est-ce qu’un anneau 
?
Notation par 
de l’opposé de 
(symétrique pour la loi [math]+[/pmath],
définitions d’anneau unitaire, commutatif.
(le neutre pour la loi 
) est un élément absorbant.
et 
dans le cas d’un anneau unitaire
Règles de calcul dans un anneau… formule du binôme dans le cas d’un anneau commutatif ou de deux éléments qui commutent.