Semaine 4, L2 Intégrales
30 octobre 2007Théorème. Si  est une fonction continue positive
sur l’intervalle
est une fonction continue positive
sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) alors
alors
 (au sens est la fonction nulle) si et seulement si
(au sens est la fonction nulle) si et seulement si
 .
.
IV) Dérivation et intégration.
Théorème (fondamental de l’analyse). Si  est
une fonction intégrable sur l’intervalle
est
une fonction intégrable sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) alors la fonction
alors la fonction  définie sur
définie sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) par
par  (bien définie car
(bien définie car  est
intégrable sur
est
intégrable sur ![delim{[}{a,x}{]} delim{[}{a,x}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_ec10a96e5f06b57469aa6c0dae09fe15.png) pour tout
pour tout  )
est une fonction continue sur
)
est une fonction continue sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) .
.
De plus si  est continue en
est continue en  alors
alors  est dérivable en
est dérivable en  et
et  .
.
Définition. Si  est une fonction continue définie
sur
est une fonction continue définie
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) , une primitive
, une primitive  est une
fonction telle que
est une
fonction telle que  pour tout
pour tout 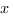 dans
dans ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) .
.
Théorème. Toute fonction continue admet une primitive. De plus si
 est une primitive alors il existe
est une primitive alors il existe  dans
dans
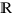 tel que
tel que  pour tout
pour tout 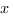 dans
dans ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) où
où  .
.
Applications.
Formule d’intégration par partie
Exemples :
Formule de changement de variables
Remarque. Attention pour le calcul de primitive il faut s’assurer
que la fonction 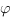 dans le changement de variable est
une bijection.
dans le changement de variable est
une bijection.
Exemples :
Formule de Taylor-Lagrange avec reste intégrale.
Proposition. Soit  une fonction
une fonction  continument dérivable
sur
continument dérivable
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) . Alors on a
. Alors on a

