Semaine 5, L2 Algèbre
30 octobre 2007suite sur les anneaux
Définition. Qu’est-ce qu’un morphisme d’anneau, isomorphisme, morphisme d’anneau unitaire ?
Définition. Qu’est-ce qu’un sous-anneau ?
Proposition. L’intersection d’une famille de sous-anneau est un sous-anneau.
Conséquence, définition. Le sous-anneau engendré par une partie non vide 
est l’intersection des sous-anneaux qui contiennent la partie .
Deux sous anneaux triviaux: 
lui-même et 
2) Diviseur de zéro — anneau intègre
Dans la suite les anneaux considérés seront commutatifs et unitaires.
Définition. Un élément 
différent de 
est diviseur
de zéro s’il existe un élément 
différent de tel que
.
Proposition Tout élément est régulier pour la loi 
si seulement
si il n’est pas diviseur de zéro.
Définition. Un anneau 
est un anneau intègre s’il est unitaire commutatif et ne possède
aucun diviseur de zéro.
Remarque Dans un anneau intègre tout élément différent de est régulier.
3) Corps - élément inversible
Définition Qu’est-ce qu’un corps ?, un sous-corps ?
4) Idéal — anneau quotient.
Définition. Qu’est qu’un idéal ?
Théorème. L’image réciproque d’un idéal par un morphisme d’anneau est un idéal.
Remarque. Cependant l’image d’un idéal n’est pas en général un idéal. Chercher un contre-exemple !
Proposition. L’intersection d’une famille d’idéaux est un idéal.
Définition. Soit une partie non vide de . On appelle idéal
engendré par l’intersection des idéaux contenant .
Anneau quotient
Définition Si 
idéal de l’anneau on définit
la relation “ congru à modulo ” (
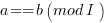) par 
.
Proposition. La relation ainsi définie est une relation d’équivalence sur
compatible avec la loi 
(déjà connu d’après le cours sur les groupes) et avec
la loi .
Théorème-définition L’ensemble quotient 
muni des lois 
et 
est un anneau appelé anneau quotient.
Exemple si 
, 
.
Divisibilité — anneau principal — 
Définition. Que veut dire divise dans un anneau intègre ?
Proposition. 
où 
désigne l’idéal engendré par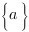 
.