Olivier Guibé Nouveau site http://olivier.guibe.free.fr

« Précédent—Suivant »

Semaine 5, L2 Intégrales

30 octobre 2007

suite et fin : Inégalité de Taylor-Lagrange

V) Interprétation géométrique et calcul approché.

1) Aire (algèbrique) du domaine 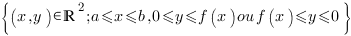représente .

2)Calcul approché, méthode des rectangles et des trapèzes, estimations de l’erreur sous des hyphothèses de régularité sur .

Chapitre 2 — Intégrales généralisées ou intégrales impropres

Intégrales généralisées.

1) Définitions.

Soit une fonction définie de l’intervalle 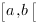dans 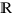avec ou . On dit que est localement intégrable sur 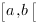si pour tout est intégrable .

Définition. (intégrale une seule fois impropre) Soit une fonction localement intégrable sur 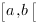. On dit que est intégrable au sens généralisé de Riemann si existe. On note cette limite .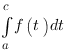

Remarque. Si est Riemann intégrable sur l’intervalle alors (bien sûr) la restricition de sur 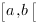est intégrable au sens généralisé de Riemann.

Remarque. Dans toute la suite (exercice, examen, etc) il faudra montrer que l’existence de cette intégrale généralisée avant tout calcul, manipulation, etc.

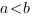Remarque. Définition analogue pour un intervalle du type avec ou .