Semaine 2, L2 Intégrales
8 octobre 2007Relation de Chasles. Soit  une fonction définie de
une fonction définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans
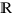 . Soit
. Soit 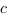 tel que
tel que  . Alors
. Alors  est Riemann
intégrable sur l’intervalle
est Riemann
intégrable sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) si et seulement si
si et seulement si  est Riemann
intégrable sur l’intervalle
est Riemann
intégrable sur l’intervalle ![delim{[}{a,c}{]} delim{[}{a,c}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_dbb7ec04d57ea50d102eedaa2ba62a6c.png) et sur
et sur ![delim{[}{c,b}{]} delim{[}{c,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_42b3f6b154cb5acc622f91781ede862d.png) . De plus, dans ce cas, on
a
. De plus, dans ce cas, on
a

Notation. Définition Si  est une fonction Riemann intégrable sur l’intervalle
est une fonction Riemann intégrable sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) alors on note
alors on note 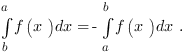
Exemples. Il n’y a pas que des fonctions Riemann intégrables !
Exemple 1. La fonction  définie sur
définie sur ![delim{[}{0,1}{]} delim{[}{0,1}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_3292a1df929141f907dd18a77d2ac41e.png) par
par  si
si 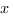 est dans
est dans  et
et  sinon n’est pas Riemann intégrable.
sinon n’est pas Riemann intégrable.
Exemple 2. La fonction  définie sur
définie sur ![delim{[}{0,1}{]} delim{[}{0,1}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_3292a1df929141f907dd18a77d2ac41e.png) par
par  si
si 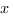 est dans
est dans  ,
,  et
et  si
si  avec
avec 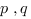 dans
dans  premier entre eux, est Riemann intégrable.
premier entre eux, est Riemann intégrable.
Remarque. La composée de deux fonctions Riemann intégrables n’est pas nécessairement Riemann intégrable.
Exercice. Si  est Rieman intégrable de
est Rieman intégrable de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 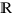 et si
et si 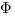 est une fonction continue de
est une fonction continue de 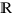 dans
dans 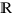 alors
alors  est Riemann intégrable. On pourra commencer par le cas plus simple d’une fonction
est Riemann intégrable. On pourra commencer par le cas plus simple d’une fonction  positive et démontrer que
positive et démontrer que 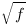 est Riemann intégrable.
est Riemann intégrable.
3) Classes de fonctions Riemann intégrables
Les fonctions croissantes sont Riemann intégrables.
Les fonctions continues sur un intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) sont Riemann intégrables sur ce même intervalle.
sont Riemann intégrables sur ce même intervalle.
