Semaine 5, L2 Algèbre
octobre 30th, 2007
suite sur les anneaux
Définition. Qu’est-ce qu’un morphisme d’anneau, isomorphisme, morphisme d’anneau unitaire ?
Définition. Qu’est-ce qu’un sous-anneau ?
Proposition. L’intersection d’une famille de sous-anneau est un sous-anneau.
Conséquence, définition. Le sous-anneau engendré par une partie non vide  est l’intersection des sous-anneaux qui contiennent la partie
est l’intersection des sous-anneaux qui contiennent la partie  .
Deux sous anneaux triviaux:
.
Deux sous anneaux triviaux:  lui-même et
lui-même et 
2) Diviseur de zéro — anneau intègre
Dans la suite les anneaux considérés seront commutatifs et unitaires.
Définition. Un élément  différent de
différent de  est diviseur
de zéro s’il existe un élément
est diviseur
de zéro s’il existe un élément  différent de
différent de  tel que
tel que
 .
.
Proposition Tout élément  est régulier pour la loi
est régulier pour la loi  si seulement
si il n’est pas diviseur de zéro.
si seulement
si il n’est pas diviseur de zéro.
Définition. Un anneau  est un anneau intègre s’il est unitaire commutatif et ne possède
aucun diviseur de zéro.
est un anneau intègre s’il est unitaire commutatif et ne possède
aucun diviseur de zéro.
Remarque Dans un anneau intègre tout élément différent de  est régulier.
est régulier.
3) Corps - élément inversible
Définition Qu’est-ce qu’un corps ?, un sous-corps ?
4) Idéal — anneau quotient.
Définition. Qu’est qu’un idéal ?
Théorème. L’image réciproque d’un idéal par un morphisme d’anneau est un idéal.
Remarque. Cependant l’image d’un idéal n’est pas en général un idéal. Chercher un contre-exemple !
Proposition. L’intersection d’une famille d’idéaux est un idéal.
Définition. Soit  une partie non vide de
une partie non vide de  . On appelle idéal
engendré par
. On appelle idéal
engendré par  l’intersection des idéaux contenant
l’intersection des idéaux contenant  .
.
Anneau quotient
Définition Si  idéal de l’anneau
idéal de l’anneau  on définit
la relation “
on définit
la relation “ congru à
congru à  modulo
modulo  ” (
” (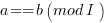 ) par
) par  .
.
Proposition. La relation ainsi définie est une relation d’équivalence sur  compatible avec la loi
compatible avec la loi  (déjà connu d’après le cours sur les groupes) et avec
la loi
(déjà connu d’après le cours sur les groupes) et avec
la loi  .
.
Théorème-définition L’ensemble quotient  muni des lois
muni des lois  et
et  est un anneau appelé anneau quotient.
est un anneau appelé anneau quotient.
Exemple si  ,
,  .
.
Divisibilité — anneau principal — 
Définition. Que veut dire  divise
divise  dans un anneau intègre ?
dans un anneau intègre ?
Proposition.  où
où  désigne l’idéal engendré par
désigne l’idéal engendré par 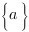 .
.
Semaine 4, L2 Intégrales
octobre 30th, 2007
Théorème. Si  est une fonction continue positive
sur l’intervalle
est une fonction continue positive
sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) alors
alors
 (au sens est la fonction nulle) si et seulement si
(au sens est la fonction nulle) si et seulement si
 .
.
IV) Dérivation et intégration.
Théorème (fondamental de l’analyse). Si  est
une fonction intégrable sur l’intervalle
est
une fonction intégrable sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) alors la fonction
alors la fonction  définie sur
définie sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) par
par  (bien définie car
(bien définie car  est
intégrable sur
est
intégrable sur ![delim{[}{a,x}{]} delim{[}{a,x}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_ec10a96e5f06b57469aa6c0dae09fe15.png) pour tout
pour tout  )
est une fonction continue sur
)
est une fonction continue sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) .
.
De plus si  est continue en
est continue en  alors
alors  est dérivable en
est dérivable en  et
et  .
.
Définition. Si  est une fonction continue définie
sur
est une fonction continue définie
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) , une primitive
, une primitive  est une
fonction telle que
est une
fonction telle que  pour tout
pour tout 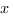 dans
dans ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) .
.
Théorème. Toute fonction continue admet une primitive. De plus si
 est une primitive alors il existe
est une primitive alors il existe  dans
dans
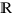 tel que
tel que  pour tout
pour tout 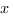 dans
dans ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) où
où  .
.
Applications.
Formule d’intégration par partie
Exemples :
Formule de changement de variables
Remarque. Attention pour le calcul de primitive il faut s’assurer
que la fonction 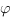 dans le changement de variable est
une bijection.
dans le changement de variable est
une bijection.
Exemples :
Formule de Taylor-Lagrange avec reste intégrale.
Proposition. Soit  une fonction
une fonction  continument dérivable
sur
continument dérivable
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) . Alors on a
. Alors on a

Semaine 4, L2 Algèbre
octobre 22nd, 2007
Théorème. Toute permutation se décompose en produit de cycles à supports disjoints. De plus si l’on exclut les
cycles triviaux d’ordre 1, cette décomposition est unique à l’ordre près.
Preuve non faite en cours, idée sur un exemple et document donné pour cette preuve.
Proposition. Les transpositions engendrent l’ensemble des permutations, i.e. toute permutation peut se décomposer
en produit de transposition.
Pour la preuve il suffit de montrer que tout cycle se décompose en produit de transposition et d’utiliser le théorème précédent.
Définition. Qu’est-ce que la signature d’une permutation ? ici on donne la définition via le nombre d’inversion, la signature est notée  .
.
Proposition. Si  sont
sont 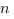 réels et
réels et 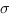 une permutation de
une permutation de  alors
alors
 .
.
Proposition. Si 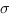 et
et  sont deux permutations alors
sont deux permutations alors  .
.
III) Anneaux
1) Définitions. Qu’est-ce qu’un anneau  ?
?
Notation par  de l’opposé de
de l’opposé de  (symétrique pour la loi [math]+[/pmath],
définitions d’anneau unitaire, commutatif.
(symétrique pour la loi [math]+[/pmath],
définitions d’anneau unitaire, commutatif.
 (le neutre pour la loi
(le neutre pour la loi  ) est un élément absorbant.
) est un élément absorbant.
 et
et 
 dans le cas d’un anneau unitaire
dans le cas d’un anneau unitaire
Règles de calcul dans un anneau… formule du binôme dans le cas d’un anneau commutatif ou de deux éléments qui commutent.
Semaine 3, L2 Intégrales
octobre 16th, 2007
III) Fonctions à valeurs complexes
Définition. Soit  une fonction de
une fonction de
![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) à valeurs complexes. La fonction
à valeurs complexes. La fonction
 est intégrable au sens de Riemann si et seulement
est intégrable au sens de Riemann si et seulement
 et
et  (parties réelle et
complexe de la fonction) sont intégrables au sens de Riemann
sur l’intervalle
(parties réelle et
complexe de la fonction) sont intégrables au sens de Riemann
sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) . Dans ce cas on
définit
. Dans ce cas on
définit  .
.
Propriétés. Les propriétés vues précédemment dans le cas des fonctions
à valeurs réelles subsistent. De plus on a l’inégalité pour toute
fonction à valeurs complexes intégrables sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)

IV) Cauchy-Schwarz, Minkowski et inégalité de la moyenne
1) Cauchy-Scwarz et Minkowski
Proposition, inégalité de Cauchy-Schwarz. Soient  et
et
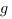 deux fonctions intégrables au sens de Riemann sur l’intervalle
deux fonctions intégrables au sens de Riemann sur l’intervalle
![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) . Alors la fonction
. Alors la fonction  est
intégrable et on a l’inégalité
est
intégrable et on a l’inégalité

Remarque. Le produit de deux fonctions intégrables est intégrable
Proposition, inégalité de Minkowski

2) Inégalité de la moyenne
Proposition. Soient  et
et 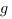 deux fonctions
intégrables au sens de Riemann sur l’intervalle
deux fonctions
intégrables au sens de Riemann sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) telles
que
telles
que  . Alors on a l’inégalité
. Alors on a l’inégalité
 Si de plus
Si de plus  est continue alors il existe
est continue alors il existe ![c in delim{[}{a,b}{]} c in delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_1d6a4d7efe65e3ff39a9e9e4bd1eda6f.png) tel
que
tel
que 
Définition. Soit  une fonction continue sur
une fonction continue sur
![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) (donc intégrable). Alors il existe
(donc intégrable). Alors il existe ![c in delim{[}{a,b}{]} c in delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_1d6a4d7efe65e3ff39a9e9e4bd1eda6f.png) tel
que
tel
que  . Cette quantité est appelée
valeur moyenne de
. Cette quantité est appelée
valeur moyenne de  .
.
Semaine 3, L2 Algèbre
octobre 12th, 2007
8 )  et groupe cyclique
et groupe cyclique
Théorème. Les sous-groupes de  sont
de la forme
sont
de la forme  ,
,  élément de
élément de 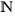 .
.
Rmq. On note  la l.c.i sur
la l.c.i sur 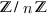 donnée
par un théorème du cours.
donnée
par un théorème du cours.
Si  alors
alors 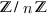 possède exactement
possède exactement 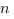 éléments,
éléments,
 ou encore noté
ou encore noté 
Application. Un groupe cyclique fini d’ordre 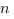 est isomorphe
à
est isomorphe
à  et un groupe cyclique infini est isomorphe à
et un groupe cyclique infini est isomorphe à  .
.
9) Le groupe symétrique
Définition. L’ensemble des permutations de  (i.e. bijection de
(i.e. bijection de  dans lui-même) muni
de la composition des applications est un groupe
appelé groupe symétrique
dans lui-même) muni
de la composition des applications est un groupe
appelé groupe symétrique  .
.
Rmq: Si  le groupe est non commutatif.
le groupe est non commutatif.
Notation-exemple. écriture d’une permutation de  sous forme de tableau, la 1ère ligne étant les éléments de
sous forme de tableau, la 1ère ligne étant les éléments de  , la seconde
ligne étant les images
, la seconde
ligne étant les images  :
:

Définitions. Soit 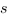 un élément de
un élément de 
-
 est point fixe de
est point fixe de 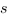 si
si  .
. - support d’une permutation noté
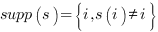 (ou
encore le complémentaire des points fixes.)
(ou
encore le complémentaire des points fixes.)
Proposition. Soient  et
et  deux éléments de
deux éléments de  .
Alors
.
Alors  .
Si de plus
.
Si de plus  et
et  sont à supports disjoints alors :
sont à supports disjoints alors :
-
 .
. -
 .
. -
 équivaut à
équivaut à  et
et  .
.
Définitions. Groupe monogène engendré par 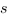 est d’ordre
fini. Ordre d’une permutation est l’ordre de
est d’ordre
fini. Ordre d’une permutation est l’ordre de  .
Si
.
Si  appartient à
appartient à  on définit l’orbite de
on définit l’orbite de  selon
selon 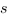 par
par  .
.
Exemple.
Définition. Cycle (ou permutation circulaire d’ordre 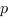 )
)
Définition. Transposition
Semaine 2, L2 Intégrales
octobre 8th, 2007
Relation de Chasles. Soit  une fonction définie de
une fonction définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans
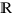 . Soit
. Soit 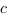 tel que
tel que  . Alors
. Alors  est Riemann
intégrable sur l’intervalle
est Riemann
intégrable sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) si et seulement si
si et seulement si  est Riemann
intégrable sur l’intervalle
est Riemann
intégrable sur l’intervalle ![delim{[}{a,c}{]} delim{[}{a,c}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_dbb7ec04d57ea50d102eedaa2ba62a6c.png) et sur
et sur ![delim{[}{c,b}{]} delim{[}{c,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_42b3f6b154cb5acc622f91781ede862d.png) . De plus, dans ce cas, on
a
. De plus, dans ce cas, on
a

Notation. Définition Si  est une fonction Riemann intégrable sur l’intervalle
est une fonction Riemann intégrable sur l’intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) alors on note
alors on note 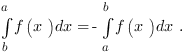
Exemples. Il n’y a pas que des fonctions Riemann intégrables !
Exemple 1. La fonction  définie sur
définie sur ![delim{[}{0,1}{]} delim{[}{0,1}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_3292a1df929141f907dd18a77d2ac41e.png) par
par  si
si 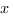 est dans
est dans  et
et  sinon n’est pas Riemann intégrable.
sinon n’est pas Riemann intégrable.
Exemple 2. La fonction  définie sur
définie sur ![delim{[}{0,1}{]} delim{[}{0,1}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_3292a1df929141f907dd18a77d2ac41e.png) par
par  si
si 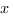 est dans
est dans  ,
,  et
et  si
si  avec
avec 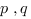 dans
dans  premier entre eux, est Riemann intégrable.
premier entre eux, est Riemann intégrable.
Remarque. La composée de deux fonctions Riemann intégrables n’est pas nécessairement Riemann intégrable.
Exercice. Si  est Rieman intégrable de
est Rieman intégrable de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 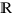 et si
et si 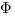 est une fonction continue de
est une fonction continue de 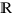 dans
dans 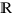 alors
alors  est Riemann intégrable. On pourra commencer par le cas plus simple d’une fonction
est Riemann intégrable. On pourra commencer par le cas plus simple d’une fonction  positive et démontrer que
positive et démontrer que 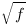 est Riemann intégrable.
est Riemann intégrable.
3) Classes de fonctions Riemann intégrables
Les fonctions croissantes sont Riemann intégrables.
Les fonctions continues sur un intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) sont Riemann intégrables sur ce même intervalle.
sont Riemann intégrables sur ce même intervalle.
Semaine 1, L2 Intégrales
octobre 5th, 2007
I] Intégrale et fonctions en escalier
1) Définitions
Définition : subdivision d’une subdivision (ou partage) d’un intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)
Définition : qu’est-ce qu’une fonction en escalier définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 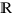 ?
?
Définition : qu’est-ce qu’une subdivision adaptée à une fonction  en escalier
en escalier
Relation d’ordre sur l’ensemble des subdivision d’un intervalle ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)
Conséquences : si 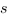 et
et  sont deux subdivisions on définit la plus fine des deux et
la plus grossière des deux. La plus fine étant “grosso-modo” la réunion des deux (attention c’est une suite ordonnée)
et la plus grossière étant l’intersection (nécessairement non vide car les deux extrémités sont des points
de la subdivision).
sont deux subdivisions on définit la plus fine des deux et
la plus grossière des deux. La plus fine étant “grosso-modo” la réunion des deux (attention c’est une suite ordonnée)
et la plus grossière étant l’intersection (nécessairement non vide car les deux extrémités sont des points
de la subdivision).
Propriétés des fonctions en escalier
Il suffit de faire un dessin pour se convaincre que si  sont deux fonctions en escalier sur
sont deux fonctions en escalier sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) et
et  un réel alors
un réel alors
-
 est une fonction en escalier
est une fonction en escalier -
 est une fonction en escalier
est une fonction en escalier -
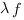 est une fonction en escalier
est une fonction en escalier -
 est une fonction en escalier
est une fonction en escalier
Remarque L’ensemble des fonctions en escalier est une algèbre
2) Intégrale d’une fonction en escalier
Définition Si  est une fonction en escalier et
est une fonction en escalier et  une subdivision adaptée à
une subdivision adaptée à  alors la quantité
alors la quantité
 où
où  est la valeur constante prise par
est la valeur constante prise par  sur l’intervalle
sur l’intervalle ![delim{]}{x_i,x_{i+1}}{[} delim{]}{x_i,x_{i+1}}{[}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_986_65c66e982f749a99da9bfc363d6b9a86.png) , ne dépend que de
, ne dépend que de  et en aucun cas de la subdvision. Cette somme est l’intégrale de
et en aucun cas de la subdvision. Cette somme est l’intégrale de  à
à  de
de  et se note
et se note  .
.
il faut bien voir/comprender/savoir démontrer que la quantité ainsi définie ne dépend
pas de la subdivision choisie !
Propriétés :
- si
 sont deux fonctions en escalier sur
sont deux fonctions en escalier sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) coïncidant sauf en un nombre fini de points alors leur intégrale sur l’intervalle sont égales
coïncidant sauf en un nombre fini de points alors leur intégrale sur l’intervalle sont égales - l’application qui à une fonction en escalier associe son intégrale est une application linéaire
-

- si
 est positive alors son intégrale l’est aussi
est positive alors son intégrale l’est aussi
Relation de Chasles. Comme la restriction d’un fonction en escalier sur ![[a,b] [a,b]](/wordpress/wp-content/plugins/phpmathpublisher/img/math_981_7be3ce2022e25e9c66f71ee324ecc5aa.png) à un sous intervalle est encore en escalier on démontre
à un sous intervalle est encore en escalier on démontre

II] Intégrabilité au sens de Riemann
1) Définition
Définition Soit  une fonction définie de
une fonction définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 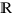 . Cette fonction est dite Riemann-intégrable si et seulement si l’une des deux conditions équivalentes est vérifiée
. Cette fonction est dite Riemann-intégrable si et seulement si l’une des deux conditions équivalentes est vérifiée
- (A) pour tout
 strictement positif il existe
strictement positif il existe  en escalier
sur
en escalier
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) telles que pour tout
telles que pour tout 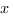 dans
dans ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) on a
on a
 et
et 
- (B) il existe deux suites de fonctions en escalier
 telles que pour tout
telles que pour tout 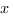 et pour tout
et pour tout 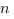 on a
on a
 et
et 
Quand une des propriétés équivalents (A) ou (B) est vérifiée et pour toute suite 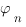 associée à
associée à  définie par (B) on démontre que la quantité
définie par (B) on démontre que la quantité 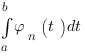 converge vers un réel qui ne dépend pas du choix de la suite
converge vers un réel qui ne dépend pas du choix de la suite 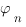 mais qui dépend uniquement de
mais qui dépend uniquement de  et est noté
et est noté
 .
.
Remarque. Si  est en escalier alors elle est intégrable au sens de Riemann (heureusement) et les notations
introduites sont compatibles.
est en escalier alors elle est intégrable au sens de Riemann (heureusement) et les notations
introduites sont compatibles.
Proposition. Si une fonction est Riemann intégrable alors elle est bornée.
Lemme. Soit  une fonction définie de
une fonction définie de ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) dans
dans 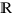 . La fonction
. La fonction  est Riemann intégrable si et seulement si pour tout
est Riemann intégrable si et seulement si pour tout  telles que
telles que
-
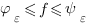 sur
sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png)
-
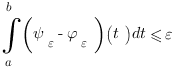
2) Propriétés
- l’application qui à une fonction Riemann-intégrable associe son intégrale est une application linéaire
- Si
 est positive et Riemann intégrable il en est de même pour son intégrale
est positive et Riemann intégrable il en est de même pour son intégrale - si
 est Riemann intégrable alors
est Riemann intégrable alors  est Riemann intégrable et
est Riemann intégrable et

- Si
 est Riemann intégrable et si
est Riemann intégrable et si  est une fonction égale à
est une fonction égale à  partout (sur
partout (sur ![delim{[}{a,b}{]} delim{[}{a,b}{]}](/wordpress/wp-content/plugins/phpmathpublisher/img/math_991.5_0e94005a5956c679066e170921261c3a.png) ) sauf en un nombre fini de points alors
) sauf en un nombre fini de points alors  est Riemann intégrable et
est Riemann intégrable et

Remarque : il faut bien comprendre que dans les deux dernières propriétés il y a d’une part une propriété qualitative
( et
et 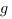 sont Riemann-intégrables) et d’autre part une propriété quantitative (une inégalité et une égalité).
sont Riemann-intégrables) et d’autre part une propriété quantitative (une inégalité et une égalité).
Semaine 2, L2 Algèbre
octobre 3rd, 2007
Bonjour
Voici ce qui a été fait en cours:
Démonstration du Théorème de Lagrange
Définition de l’ordre d’un élément
Groupe quotient
Définition. Une relation d’équivalence  est dite
compatible avec la loi
est dite
compatible avec la loi  si
si  et
et  entraînent
entraînent 
Théorème. Si  est une relation d’équivalence compatible
avec
est une relation d’équivalence compatible
avec  (
( groupe) alors l’ensemble quotient
groupe) alors l’ensemble quotient  muni de la l.c.i,
muni de la l.c.i,  , est un groupe
, est un groupe
Application. Si  est abélien et
est abélien et  sous groupe de
sous groupe de  définition de la relation
modulo
définition de la relation
modulo  (
(  ssi
ssi 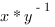 dans
dans  ), compatible avec
), compatible avec  .
.
On note 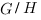 l’ensemble
l’ensemble  , qui est un groupe muni de
la loi définie dans le théorème précédent.
, qui est un groupe muni de
la loi définie dans le théorème précédent.
Description des classes d’équivalence
Exemple (détaillé?!). 
7) Décomposition canonique d’un morphisme de groupe
Théorème. Si morphisme de groupe de
morphisme de groupe de  dans
dans
 (groupes supposés abéliens) alors
(groupes supposés abéliens) alors  et
et  sont isomorphes.
sont isomorphes.
Semaine 1, L2 algèbre
octobre 2nd, 2007
Bonjour
Voici ce qui a été fait aux deux cours de la 1ère semaine.
I] Lois de composition interne
Des définitions, des définitions et beaucoup de définitions En vrac, qu’est-ce qu’un l.c.i. ? associativité, commutativité, Éléments particuliers : neutre, symétrisable, régulier ou simplifiable. Le neutre s’il existe est unique, de même pour le symétrique à condition de savoir que la loi est associative ! symétrisable entraîne simplifiable ou régulier
Partie stable, loi induite ou comment munir un sous ensemble d’un ensemble structuré de la loi induite.
Morphismes, définition
II] Groupes
1)Définition Un groupe  est un ensemble muni d’un l.c.i telle que
est un ensemble muni d’un l.c.i telle que
a) la loi  est associative
est associative
b)  possède un élément neutre
possède un élément neutre
c) tout élément de  est symétrisable
est symétrisable
2) Sous Groupes
Définition : Qu’est-ce qu’un sous groupe ?
Théorème
Soient  un groupe et
un groupe et  une partie non vide de
une partie non vide de  . Alors
. Alors
 sous groupe de
sous groupe de  ssi
ssi
(1) pour tout  dans H,
dans H,  appartient à
appartient à 
(2) pour tout 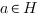 ,
,  (qui désigne le symétrique de
(qui désigne le symétrique de
 dans
dans  ) appartient à
) appartient à 
Théorème: (même hypothèse).  est un sous groupe de
est un sous groupe de  ssi
pour tout
ssi
pour tout  dans
dans  ,
,  est dans
est dans  (toujours
(toujours  désigne le symétrique de
désigne le symétrique de  dans
dans  )
)
Théorème: l’intersection d’une famille non vide de sous groupes est un sous-groupe.
Rmq-exercice: Pour l’union c’est faux (en général) !
Proposition-Définition: Le sous groupe engendré par  , une partie
non vide de
, une partie
non vide de  , est le plus petit sous-groupe au sens de l’inclusion
contenant
, est le plus petit sous-groupe au sens de l’inclusion
contenant  . Notation,
. Notation, 
Définition d’un sous-groupe monogène
3) Groupe produit ou comment on munit le produit
cartésien  d’une structure de groupe
d’une structure de groupe
Généralisation au cas d’un produit fini 
4) Morphisme de groupe
Définition
Théorème:  par un morphisme de groupe
de
par un morphisme de groupe
de  dans
dans  est le neutre de
est le neutre de 
b) l’image du symétrique est le symétrique de l’image (attention aux ensembles et notations)
c) 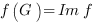 est le (sous)groupe image
est le (sous)groupe image
d)  noyau de f est un sous-groupe
noyau de f est un sous-groupe
Théorème: CNS pour qu’un morphisme de groupe soit injectif
5) Groupe fini
Définition de l’ordre d’un groupe
Définition de l’ordre d’un élément par l’ordre
du groupe engendré par 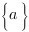
Définition d’un groupe (sous-groupe) cyclique
Théorème de Lagrange. Si  est un groupe fini
alors l’ordre de tout sous-groupe de
est un groupe fini
alors l’ordre de tout sous-groupe de  divise l’ordre de
divise l’ordre de 
Preuve la semaine prochaine !
Installation de PHPMathPublisher
septembre 6th, 2007
Pour les formules mathématiques il m’est impossible d’avoir la solution idéale, à savoir LaTeX sur le serveur puis MimeTeX.
J’ai tenté le MathML via AsciiMathMl, je ne sais pas trop ce que cela donne pour l’extérieur. Je viens d’installer une autre
possibilité : PHPMathPublisher. L’avantage par rapport à MathML est qu’il n’y pas besoin de plugin pour IE. Pour les inconvénients, les formules sont des images : sur le serveur de free ce sera nécessairement lent. Voici un exemple

« Page Précédente — Page suivante »
